1.- Un triángulo rectángulo está inscrito en una semicircunferencia con diámetro igual a 8. Uno de los catetos del triángulo rectángulo mide 5. Determina las dimensiones del triángulo rectángulo.
Para la finalidad de que se encuentre el lado que falta del triangulo.
2.- Construye un triángulo rectángulo cuyos catetos miden CM= , Cm= 45. Trazar el triángulo y la semicircunferencia circunscrita.Los catetos deben ser con las medidas que se tienen que aplicar para poder obtener el lado que falta.
domingo, 24 de enero de 2016
domingo, 17 de enero de 2016
área verde

Pasos para resolverlo:
1) Sacar el área del semicírculo:
A = π × r2
A= (3.1416....* (35 m)² ) = 3 848.46 m²
A= 3 848.46 m²/2 = 1 924.23 m²
2) Sacar el área de la 8va. parte del circulo:
A = π × r2
A= (3.1416....* (70 m)² ) = 15 393,85 m²
A= 15 393,85 m²/8 = 1 924.23 m²
3) Sacar el área del triángulo inscrito en el semicírculo:
A = (b × h) / 2
A= (70 m * 35 m) /2 = 1 225 m²
4) Restar al semicírculo el área del triángulo:
1 924.23 m² -1 225 m² = 699.23 m²
5) Dividir ese resultado entre dos:
699.23 m² /2 = 349.615 m²
6) Restar ese resultado al área sacada en el punto 2:
1 924.23 m²- 349.615 m²= 1 574. 61 m²
Y ese es la cantidad de pasto del área verde.
ÁNGULOS ENTRE PARALELOS
Ángulos entre paralelos
Observa en el dibujo que dos rectas paralelas cortadas una recta transversal crea 8 ángulos que reciben distintos nombres según la posición que ocupan:
Las recta r corta a las rectas paralelas M y N:
Los nombres de los ángulos según el lugar que ocupan reciben los nombres:
Interiores o internos:
En azul, son los que se encuentran entre las rectas paralelas.
Ángulos exteriores o externos:
Los ángulos exteriores o externos en color violeta, son los que hallan en la zona exterior de las paralelas.
Ángulos correspondientes:
Son los que se encuentran en el mismo lado de la secante, un ángulo en la parte interior y otro en el exterior de las paralelas.
Son los que se encuentran en el mismo lado de la secante, un ángulo en la parte interior y otro en el exterior de las paralelas.
Los ángulos del mismo color son correspondientes:
El ángulo a se corresponde con el ángulo a’
El ángulo b se corresponde con el ángulo b’
El ángulo c se corresponde con el ángulo c’
El ángulo d se corresponde con el ángulo d’
El ángulo a se corresponde con el ángulo a’
El ángulo b se corresponde con el ángulo b’
El ángulo c se corresponde con el ángulo c’
El ángulo d se corresponde con el ángulo d’
Teniendo en cuenta lo dicho hasta aquí y fijándonos en la figura podemos afirmar que los ángulos correspondientes son iguales entre sí.
Ángulos alternos internos
Son los que se encuentran a distinto lado de la secante y en la zona interior de las rectas paralelas:
Los ángulos internos son d’, c, b y a’. Si los tomamos alternadamente, tendríamos, por un lado, los ángulos d’ y b, y por otro, c y a’ y comprobarás que los alternos internos son iguales entre sí.
Ángulos alternos externos:
Son los que se encuentran a distinto lado de la secante y en la zona externa de las rectas paralelas:
Los ángulos externos son: a, b’, c’ y d que tomándolos alternadamente tendremos, por un lado los ángulos a y c’, y por otro, los ángulos b’ y d. Comprobarás que los ángulos alternos externos son iguales entre sí.
Propiedades Geométricas
PROPIEDADES GEOMÉTRICAS
Las figuras geométricas componen lo que está alrededor de nosotros. Pueden ser bidimensionales, como la de tu computadora, y tridimensionales, como una pelota. Cada geométrica tiene sus propiedades que la hacen diferente de otras figuras. Sin embargo, las figuras geométricas pueden compartir propiedades con otras, lo que requiere describirlas más detalladamente para distinguirlas de otras figuras.
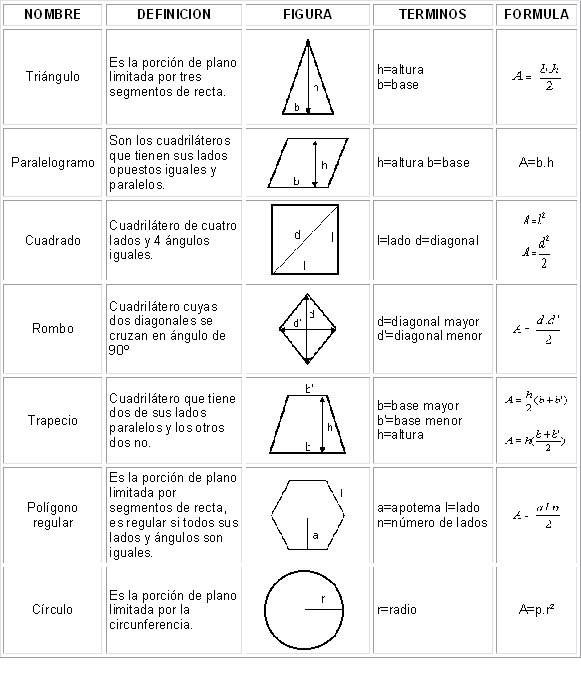

Lados
El número de lados que tiene una figura puede ayudar a determinar qué de figura geométrica es. Todas las figuras bidimensionales hechas con líneas rectas se consideran polígonos. Por ejemplo, un triángulo es una figura bidimensional que tiene tres lados. Los lados por sí solos no identifican la figura. Hay muchas figuras que tienen cuatro lados, como los cuadrados, rectángulos, rombos, trapezoides y muchas otras. Sin embargo, todas las figuras con cuatro lados se consideran cuadriláteros. Algunas figuras no tienen esquinas y por lo tanto no tienen lados distinguibles. Los círculos y los óvalos son ejemplos de figuras geométricas que no tienen lados distinguibles.
Ángulos
Las figuras que tienen esquinas, también llamadas vértices, crean ángulos que pueden medirse. Los ángulos están presentes tanto en las figuras bidimensionales como en las tridimensionales. Un ángulo puede medirse usando un transportador. Un ángulo puede ser agudo, lo que significa que mide menos de 90 grados, recto, que quiere decir que es de exactamente 90 grados, u obtuso, lo que significa que es mayor a 90 grados.
Regulares e irregulares
Las figuras bidimensionales pueden clasificarse en regulares e irregulares. Los polígonos regulares son polígonos cuyos lados y ángulos interiores son congruentes, es decir, iguales. Un triángulo equilátero es un triángulo en el que los tres lados son iguales en longitud y todos los ángulos interiores son de 60 grados, lo que lo hace un triángulo regular. No todas las figuras pueden ser regulares. Un rectángulo, por ejemplo, por definición tiene dos lados que son iguales en longitud. Un lado es más largo que el otro. Esto hace que el rectángulo sea una figura irregular.
Figuras tridimensionales
La geometría no se limita a las figuras bidimensionales. También incluye las figuras tridimensionales, llamadas también figuras sólidas. Estas figuras tienen un valor adicional de profundidad que no tienen las figuras bidimensionales. Las figuras tridimensionales se construyen con figuras bidimensionales. Por ejemplo, un cubo es una figura tridimensional que se construye con seis cuadrados ordenados en la forma de una caja. Otras figuras son una combinación de varias figuras geométricas. Un prisma es una combinación de rectángulos y triángulos.
Bases
Las figuras tridimensionales tienen bases. La base es la cara de la figura que descansa sobre un plano. Por ejemplo, una pirámide tiene una base cuadrada. Un cilindro tiene una base circular. En algunos casos, la base es igual al resto de las caras, como en el caso de un cubo. Una esfera, que se ve como una pelota, no tiene una base. Una esfera se describe como una figura en la que todos los puntos están a la misma distancia del centro.


martes, 12 de enero de 2016
ENSAYO
Argumentos a favor y en contra del rectángulo áureo


La Catedral de Notre Dame, en París, muestra varios ejemplos de la proporción áurea, más fáciles de ver en la fachada occidental de la catedral, tanto en la estructura general como en numerosas subestructuras.
El rectángulo aureo es muy estático y armonioso esta considerado que es una de las formas que mas bellas que puedes hacer en su forma se dice que si usas esta forma de hacer algo como arquitectura, artesanías o alguna obra de arte, puede ser que la gente note una diferencia a primera vista una diferencia hermosa en su vista y así llame la atención de la gente mucha gente a importante e artística y profesionales han usado este método como base de su trabajo algunos creen y algunos no pero la mayoría cree en la teoría de este rectángulo áureo por mucho tiempo se a afirmado que las porciones de este rectángulo son armoniosas por naturaleza y que. cualquier diseño que este basado en el valor=1.618033 así el rectángulo se hace ver atractivo a los espectadores se uso en la antigüedad y así se uso en estas épocas
La sección áurea nace en Roma en el que también se le es conocida como sección divina, sección de oro, proporción divina, proporción dorada, canon áureo, regla de oro o número de oro . En sí la sección áurea es un equilibrio completo, representa un significativo número puesto que es un intento por encontrar la explicación matemática a la belleza con el fin de encontrar la cifra ideal. La sección áurea también se entiende que es la proporción o un equilibrio que ocurre entre dos segmentos de una recta al dividir ésta medida y extrema razón
Un rectángulo cuyos lados están en una proporción igual a la razón áurea es llamado un rectángulo áureo. Este es un rectángulo muy especial como veremos. Los griegos lo consideraban de particular belleza y lo utilizaron asiduamente en su arquitectura. Al parecer a la mayoría de las personas también les parece más agradable a la vista un rectángulo con esas proporciones entre sus lados, inconscientemente se diseñan infinidad de cosas que resultan tener la forma de un rectángulo áureo. El rectángulo áureo tiene una propiedad muy interesante. A partir de él podemos obtener una infinidad de nuevos rectángulos áureos. El proceso es iterativo (repercusivo diría alguien dedicado a la computación) y consiste en quitar a cada rectángulo áureo un cuadrado, la superficie que queda luego de hacer esto es un nuevo rectángulo áureo.
Es posible también aplicar el proceso a la inversa: a partir de un rectángulo áureo, puede construirse otro más grande añadiéndole un cuadrado de lado igual al lado mayor del rectángulo original.
El rectángulo de Euclides
Se trata de una de las demostraciones más conocidas desde la antigüedad. El rectángulo cuyos vértices se definen por los puntos AEFD se define como áureo debido a que sus lados mayores AE y su lado corto AD presentan la proporción del número áureo. El matemático griego Euclides, en su proposición 2.11 de la obra Los Elementos obtiene su construcción. Siendo el triángulo GBC Pitagórico, se tiene que GC (la hipotenusa) tiene como valor:
Con centro en G, prolongando hasta la recta AE, se obtiene por intersección el punto E, y por lo tanto:
con todo ello se puede ver que resulta evidente que los lados:
de donde, finalmente:
Por otra parte, los rectángulos AEFD y BEFC son semejantes, de modo que este último es asimismo un rectángulo áureo.
El rectángulo áureo fue calificado por los griegos de la clásica Hélade como una de las figuras geométricas más bellamente estructuradas. Por un largo lapso de siglos, los arquitectos utilizaron este cuadrilátero de noble proporción para la planeación de templos, rascacielos y edificaciones de diversa índole. Los compatriotas de Sócrates construyeron el Partenón de Atenas en el siglo V a.C. El rectángulo que encierra la fachada delantera es un rectángulo áureo.
El origen exacto del término sección áurea es bastante incierto. Generalmente se sitúa en Alemania, en la primera mitad del S. XIX. Muchos han sido los artistas, humanistas y matemáticos que lo han tratado, aunque bajo distinto sobrenombre y con distinta disposición. Otros nombres que recibe son sección divina, sección de oro, proporción divina, proporción dorada, canon áureo, regla de oro o número de oro. Sección áurea es simplemente una proporción concreta. Esta proporción ha desempeñado un importante papel en los intentos de encontrar una explicación matemática a la belleza, de reducir ésta a un número, de encontrar “ la cifra ideal ". De esta proporción se hablaba ya desde muy antiguo, los egipcios la descubrieron buscando medidas que les permitieran dividir la tierra de forma exacta. De Egipto pasó a Grecia y de allí a Roma. Pitágoras (569 a.C.) escogió como símbolo para su Escuela la estrella pentagonal, figura geométrica que muestra en todas sus relaciones la sección áurea y se cree que a partir de esta figura llegaron a la noción de inconmensurabilidad y al conocimiento de los números inconmensurables, tales como el que ahora nos ocupa. Platón (428-347 a.C.) hace referencia a ella en el Timeo y dice “es imposible combinar bien dos cosas sin una tercera, hace falta una ligazón entre ellas que las ensamble, la mejor ligazón para esta relación es el todo...”. Euclides (450-380 a. C.), matemático griego, en su obra principal Elementos, extenso tratado de matemáticas sobre geometría plana, proporciones, propiedades de los números, magnitudes inconmensurables y geometría del espacio, nos revela la primera fuente documental importante sobre esta sección, su cálculo y trazado geométrico. Más tarde, Vitruvio, arquitecto romano, vuelve a tratarla en sus Diez libros de arquitectura.
El rectángulo áureo en la antigüedad
Si traducimos la proporción áurea en formas geométricas, observaremos que describe mágicamente muchas de las pautas que vemos en la naturaleza. Los arquitectos la utilizaban para crear edificios de excelente simetría.
Podemos ver como se expresa Fi en las pirámides de Egipto, el Partenón de Atenas y las catedrales góticas europeas; podemos percibir cómo los artistas y artesanos de todas las épocas la utilizan, y podemos verla como descripción perfecta de los principios del crecimiento y el dinamismo en la naturaleza.
El hecho de que los griegos y posteriormente artistas de todas las épocas hayan adoptado esta proporción como modelo de armonía y de belleza, ya sería motivo suficiente para tratar este número tan extraño con respeto.
Artistas y matemáticos como Lucca Pacioli, Leonardo Da Vinci o como Alberto Durero han designado a este número con nombre tan expresivos como sección áurea, razón áurea o divina proporción. Desde el Renacimiento, muchos pintores han utilizado en sus obras maestras dimensiones relacionadas con la razón áurea
Los griegos ya lo conocían, está presente en muchas de sus
manifestaciones artísticas, sobre todo en sus templos y sus esculturas.
La primera aparición del número de oro en la arquitectura fue construida hacia el año 2600 A.C en la pirámide de Keops.
Erodeto, famoso historiador griego del siglo quinto antes de cristo cuenta que los sacerdotes egipcios le había mostrado el hecho de que las dimensiones de la pirámide eran tales que el cuadrado de la altura total era exactamente igual al área de una de las caras, este dato atribuible a un exceso de meticulosidad del arquitecto egipcio no es en sí una casualidad, pero analicemos las características geométricas que se deducen, y podemos descubrir con asombro que los egipcios hace tres mil años ya conocían y aplicaban el número áureo.
La espiral logarítmica de la concha del nautilo
Convirtamos ahora los números en cuadrados. Pongamos dos iguales, uno junto a otro, de cualquier tamaño, cuyos lados tomaremos como unidad. Encima de ellos, dibujemos otro cuyo lado sea el doble de los anteriores. A la derecha, añadamos otro más, con el triple de lado. Debajo, el correspondiente a 5, y así sucesivamente, de modo que cada nuevo cuadrado tenga de lado la suma de los dos cuadrados anteriores. Si ahora dibujamos un cuarto de circunferencia dentro de cada cuadrado (empezando por el primero), como en la fotografía de la caracola del comienzo del reportaje, tendremos una espiral logarítmica que es, justamente, la que presenta la concha del nautilo.
Ahora coja un lápiz y trace una línea que vaya desde el centro al exterior.Fíjese en dos puntos en los que esta línea corte a la concha, con la única condición de que la espiral haya dado una vuelta completa entre ambos. Comprobará que el más exterior está 1,618 veces más lejos del centro que el del interior. Esto quiere decir que el factor de crecimiento de la concha es el número áureo.
El mejor sistema de ordenación posible
¿Por qué este gusto de la naturaleza por la sucesión de Fibonacci? Hojas, pétalos y semillas se ordenan en las plantas siguiendo un ángulo fijo porque éste es el mejor sistema de empaquetamiento, aunque la planta crezca. Si colocamos el número áureo de hojas por vuelta en el tallo obtenemos el mejor empaquetamiento para que reciban todas ellas el máximo de luz sin que unas se oculten a otras y, en el caso de las flores, la mejor exposición paras atraer a los insectos polinizadores. Los números de Fibonacci son la mejor aproximación que existe al número áureo. Visto todo esto, no resulta sorprendente que el Partenón pueda enmarcarse en un rectángulo áureo -aquél en el que el cociente de su longitud por su altura sale el número áureo-. Igual sucede con las tarjetas de crédito. ¿Acaso hay algo más bello que una Visa sin límite de gasto?
Ejemplos:
por ejemplo en el árbol familiar de cualquier zángano de un panal. Éste nace del huevo no fertilizado de la reina, luego tiene una madre, pero no tiene padre. Por el contrario, tanto la reina (la única que puede poner huevos) como las obreras nacen del huevo fertilizado por un macho. Tienen, por tanto, padre y madre. Teniendo esto en mente, el árbol familiar de un zángano queda como sigue: tiene 1 madre, 2 abuelos (macho y hembra), 3 bisabuelos (dos de la familia de la abuela y uno de la del abuelo), 5 tatarabuelos, 8 tataratatarabuelos...
Sección aurea en la naturaleza
La lista de formas orgánicas en las que encontramos la sección áurea podría ser interminable (algo de esto hemos intuido en el desarrollo del trabajo: las proporciones del cuerpo humano, la forma espiral de la concha del nautilus, etc.), pero aquí me limitaré a exponer la relación de ésta con algunas especies vegetales.
Algunas flores tienen la particularidad de crecer siguiendo tramas impensables que nos hacen pensar en un "Dios geómetra", por ejemplo, los flósculos de la margarita, crecen en los puntos de contacto de dos conjuntos de espirales que se mueven en direcciones opuestas, una en el mismo sentido y otra en contrario al de las agujas del reloj. El centro del girasol también se compone de flósculos que crecen siguiendo espirales logarítmicas y equiangulares y que se mueven en direcciones opuestas. El patrón estructural de una flor de cardo comparte también esta forma espiral.
La cola del camaleón.
Esta es la cola de un camaleón. Parece decirnos con su cola enroscada algo así como: "Yo también puedo crear algo parecido a una espiral de oro, sin un título en matemáticas superiores. Es muy sencillo. Simplemente comienzo con una cola, que es básicamente un cono largo y delgado, y la enrollo con fuerza. El resultado es tan bueno como el caparazón del nautilo por el que todo el mundo hace tanto escándalo".
Arte Oriental
Artesanía: En la artesanía oriental también podemos encontrar en las alfombras en los tejidos las proporciones áureas. Cerámica: En el oriente realizan jarrones con diseños de espirales están inspirados en la sección áurea, más que por cómo están pintado los jarrones es más bien su estructura ,comienza con una boquilla y termina con una anchura a lo último de la base y es lo que se destaca entre los jarrones del Oriente y de los demás lugares. Escultura: Una de las esculturas más famoso del Oriente es el Buda puesto que demuestra cómo se le encuadra los rectángulos áureos uno dentro del otro. También hay otros tipos de arte como son el arte romano, el arte griego, el arte islámico, el arte gótico, el arte renacentista, el arte barroco, el arte del siglo XVIII, el arte del siglo XIX, el arte en el siglo XX, el arte en castilla-la mancha, y así podremos encontrar distintos tipos de artes y en que todas se relacionan con la proporción áurea.
Qué significa phi? Conchas y pétalos de flores
La proporción áurea sólo es una manera de relacionar dos cantidades dadas, como la altura de un edificio en relación con su longitud con una ecuación bastante sencilla. Esta relación se llama phi (no confundir con el número Pi), por el gran escultor Fidias (phi se pronuncia “fi”). El resultado es 1,618 e infinitos decimales más. Y es el símbolo de la belleza y de Dios.

Una “espiral áurea” es la que se aleja de su punto central en un factor de phi por cada cuarto de giro. Un ejemplo bello y fácil de entender es el caparazón del Nautilus pompilus, un miembro de la familia de los pulpos. Pero este ejemplo solo se usa para que entendamos tal proporción porque es muy visual. En realidad no se ajusta perfectamente a tales parámetros, como demostró en 1999 el matemático Clement Falbo. Para encontrar un ejemplo fidedigno de proporción aúrea entonces deberemos contemplar la concha de un abulón, aunque no sea tan fotogénica.
También podemos hallar esta proporción en la disposición de los pétalos de las flores, la distribución de las hojas de los árboles, la cantidad de espirales de una piña o la disposición de las hojas de las alcachofas. Y si saltamos al cuerpo humano: la distancia entre el ombligo y la planta de los pies de una persona, respecto a su altura total.
El arquitecto Le Corbusier se inspiró en la proporción áurea para diseñar el edificio de la ONU de Nueva York, que consiste en un rectángulo áureo que, a su vez, tiene marcas distintivas que lo dividen de nuevo según la proporción áurea.

La Catedral de Notre Dame, en París, muestra varios ejemplos de la proporción áurea, más fáciles de ver en la fachada occidental de la catedral, tanto en la estructura general como en numerosas subestructuras.
ARQUITECTURA ANTIGUA GRECIA Y ROMA.
A partir de aquí empieza a estudiarse la arquitectura a través de que empiezan a salir los primeros arquitectos y así los primeros libros arquitectónicos, Hola arquitecto que sobresale de todos es llamado el vitruvio en el que menciona tiene que la arquitectura depende del orden, de la disposición, la propiedad, la euritmia, y la simetría. Dando así esta última concordancia a las proporciones del conjunto.
ARQUITECTURA GÓTICA
El arte gótico occidental europeo está compuesta entre lo romántico y el renacimiento y esto es un arte que se le considera clásico.
ARQUITECTURA EN LOS SIGLOS XIX-XX
Dentro de estos años de 1852 nace un modernismo en el cual se encuentra Anthony Gaudí en el que es el iniciador y máximo representante del mismo en Cataluña su obra que fue muy reconocida fue la sagrada familia de Barcelona, su obra era un templo en el cual en su interior tenía una escalera haciendo semejanza a una concha del nautilus.
LE CORBUSIER
Este personaje fue muy fundamental para la arquitectura pues consideró la naturaleza como encarnación de todo lo verdadero, bello sano y original todo esto lo llevó a cabo a lo largo de su vida pues giraba entorno en dos conceptos naturaleza y geometría, estas dos partes le dieron una creencia deliciosa en la naturaleza. Este personaje realiza una serie de investigaciones y es como elabora un sistema de medidas y proporciones cuya validez sería independiente de las diferentes convenciones en uso y que sin esfuerzo podiatra trasladarse del sistema métrico a medidas anglosajonas, este sistema lo llamó modulador. El modulador propone un denominador común de las dimensiones del hombre y de la geometría elemental es decir un hombre de pie, con el brazo alzado y el ombligo situado justo en medio,se haya inscrito en dos rectángulos de 1.13m de altura, y sumando los dos rectángulos da un resultado de 2. 26 m y esto es la dimensión básica de una habitación
domingo, 10 de enero de 2016
Triángulo de Herón y Rectángulo Áurea
HERÓN DE ALEJANDRÍA
Formula de Herón
Fue un matemático científico griego que fue considero como ingeniero fue el inventor de la maquina de vapor, a partir del siglo XVlll muchas maquinas empezaron a trabajar con energía de vapor,después de algunos siglos fueron las posibilidades energéticas. Da la explicación de la ventosa y al igual que Filón, emplea una maquina de aire caliente para impulsar el agua. Herón se ha echo celebre sobre todo por eolipila que, por primera vez utilizaba la fuerza impulsiva de vapor de agua de la reacción.
Formula de Herón
En geometría la fórmula de Herón, atribuida al matemático griego, da el área de un triángulo conociendo con las longitudes A,B y C.
- enseguida una practica en AUTO CAD, donde se presentara el triángulo de Herón donde con círculos dala altura de el triángulo:
- la practica,se dieron las medidas del triangulo donde la base es 12 cm y los lados del triángulo tiene una medida de 10.5 cm y 8 cm donde se pide la altura del triángulo pero se insertan de cada punto centro cada medida del triangulo, se trazan los dos círculos y se unen las lineas y se forma el triángulo y se saca la altura que es lo que se pide y las circunferencias que son las van hacer unir los puntos.
- Rectángulo Áureo
- Este rectángulo en auto cad se realizó con base a círculos y una línea en donde se dividen con los puntos de cada circunferencia, que divide que así te da cada punto para el trazo de cada línea y así obtener la medida de los lados del rectángulo Áureo, y así también obtener la medida PHI=1.1618.
-
- El rectángulo Áureo o dorado es un rectángulo que posee una proporcionalidad entre sus lados iguales es decir es aquel rectángulo que subtrae la imagen de un cuadrado igual al de su lado menor, es igualmente un rectángulo dorado, por un largo lapso de los siglos los arquitectos utilizaron este cuadrilátero de noble proporción para la planeación de templos y edificaciones de diversa índole. La norma DIN 476 define la medida del DIN A4 y otros tamaños de papel el DIN y sus derivados A3 A2 no mantienen las proporciones del rectángulo dorado si no mantiene la relación =1.4142.
- La razón dorada de acuerdo con el matemático divulgador científico Mario Greco desde la publicación Bruno Miere titulada Divina Proportione in 1509, la razón dorada aparece escrita en la arte y de arquitectura que muchos artistas y arquitectos emplearon en este gran descubrimiento y así hicieron cantidad de descubrimientos y diseños por considerarlo estéticamente agradable.

Suscribirse a:
Comentarios (Atom)











